Building Recommender Systems - Part 2: Matrix Factorization & Factorization Machines

Published on December 16, 2025

Introduction

In Part 1, we built content-based and collaborative filtering recommenders. While these work well for small datasets, they struggle with scale and sparsity. Enter **Matrix Factorization**—the technique that powered Netflix's $1M prize-winning recommendation algorithm.

In this part, we'll explore:

Matrix Factorization (SVD, ALS): Decomposing the user-item matrix into latent factors

Factorization Machines: Incorporating side features (user age, item category, time) for better predictions

Implicit Feedback: Handling clicks, views, and other non-rating signals

Production Optimization: Making these algorithms fast and scalable

The Problem with Collaborative Filtering

Recall from Part 1 that collaborative filtering uses a user-item rating matrix. The problem? Sparsity.

python

# Typical user-item matrix
#        Movie1  Movie2  Movie3  Movie4  Movie5
# User1    5.0     NaN     NaN     4.0     NaN
# User2    NaN     3.0     NaN     NaN     5.0
# User3    4.0     NaN     2.0     NaN     NaN
# User4    NaN     NaN     5.0     3.0     NaN

# Problems:
# 1. 90-99% of entries are missing (NaN)
# 2. Computing similarity becomes unreliable
# 3. Memory inefficient (storing all pairs)
# 4. Doesn't scale to millions of users/items

Matrix Factorization solves this by learning latent representations.

Matrix Factorization: The Core Idea

Instead of storing a huge sparse matrix, we learn compact representations (embeddings) for users and items.

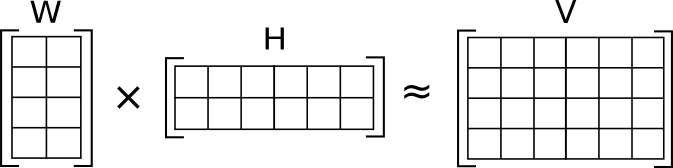
Matrix Factorization

Mathematical Foundation

Given a rating matrix R (users × items), we factorize it into:

R ≈ U × I^T

Where:

**U** is the user matrix (users × k latent factors)

**I** is the item matrix (items × k latent factors)

**k** is much smaller than users or items (typically 10-200)

Example:

python

# Instead of storing 1M users × 100K items = 100B values
# We store: (1M × 50) + (100K × 50) = 55M values
# That's a 1800x reduction!

# Predicted rating for user u and item i:
rating_pred = np.dot(user_embedding[u], item_embedding[i])

What Do Latent Factors Mean?

Latent factors capture hidden patterns in user preferences. For movies, they might represent:

Factor 1: "How much does this movie appeal to kids?"

Factor 2: "How action-packed is this movie?"

Factor 3: "How critically acclaimed?"

Factor 4: "How recent/trendy?"

Users and items are both embedded in this same latent space, allowing meaningful comparisons.

Implementing SVD-Based Matrix Factorization

Let's implement using Singular Value Decomposition (SVD).

Step 1: Setup

python

import pandas as pd
import numpy as np
from scipy.sparse.linalg import svds
from sklearn.metrics import mean_squared_error

# Load MovieLens data
ratings = pd.read_csv('ratings.csv')

# Create user-item matrix
R = ratings.pivot(index='userId', columns='movieId', values='rating').fillna(0)
R_matrix = R.values

# Normalize by subtracting mean rating for each user
user_ratings_mean = np.mean(R_matrix, axis=1)
R_normalized = R_matrix - user_ratings_mean.reshape(-1, 1)

print(f"Matrix shape: {R_normalized.shape}")
# Output: Matrix shape: (610, 9724)

Step 2: Perform SVD

python

# Perform SVD with k latent factors
k = 50  # Number of latent factors

# SVD factorization: R = U * Sigma * Vt
U, sigma, Vt = svds(R_normalized, k=k)

# Convert sigma to diagonal matrix
sigma = np.diag(sigma)

print(f"U shape (users × factors): {U.shape}")        # (610, 50)
print(f"Sigma shape (factors × factors): {sigma.shape}")  # (50, 50)
print(f"Vt shape (factors × items): {Vt.shape}")      # (50, 9724)

Step 3: Make Predictions

python

# Reconstruct the full matrix
predictions = np.dot(np.dot(U, sigma), Vt) + user_ratings_mean.reshape(-1, 1)

# Convert to DataFrame
predictions_df = pd.DataFrame(predictions, columns=R.columns, index=R.index)

def recommend_movies(user_id, num_recommendations=10):
    """
    Get top N movie recommendations for a user

    Args:
        user_id: User ID to generate recommendations for
        num_recommendations: Number of movies to recommend

    Returns:
        DataFrame with recommended movies
    """
    # Get user's predicted ratings
    user_row_number = user_id - 1  # Assuming user IDs start at 1
    sorted_user_predictions = predictions_df.iloc[user_row_number].sort_values(ascending=False)

    # Get movies the user has already rated
    user_data = ratings[ratings['userId'] == user_id]
    user_rated = user_data['movieId'].values

    # Filter out already rated movies
    recommendations = sorted_user_predictions[~sorted_user_predictions.index.isin(user_rated)]

    # Get top N
    top_recommendations = recommendations.head(num_recommendations)

    # Merge with movie titles
    movie_info = movies[['movieId', 'title', 'genres']]
    recommendations_df = pd.DataFrame({
        'movieId': top_recommendations.index,
        'predicted_rating': top_recommendations.values
    })
    recommendations_df = recommendations_df.merge(movie_info, on='movieId')

    return recommendations_df

# Test recommendations
user_recs = recommend_movies(user_id=1, num_recommendations=5)
print(user_recs)

Expected Output:

code

   movieId  predicted_rating                      title                genres
0     2571              4.85  Matrix, The (1999)        Action|Sci-Fi|Thriller
1      318              4.78  Shawshank Redemption      Crime|Drama
2      858              4.72  Godfather, The (1972)     Crime|Drama
3     1196              4.68  Star Wars: Episode V     Action|Adventure|Sci-Fi
4     2959              4.65  Fight Club (1999)        Action|Crime|Drama

Step 4: Evaluate Performance

python

# Split data into train and test
from sklearn.model_selection import train_test_split

train_data, test_data = train_test_split(ratings, test_size=0.2, random_state=42)

# Build training matrix
R_train = train_data.pivot(index='userId', columns='movieId', values='rating').fillna(0)
R_train_matrix = R_train.values

# Normalize and factorize
user_mean = np.mean(R_train_matrix, axis=1)
R_train_norm = R_train_matrix - user_mean.reshape(-1, 1)

U, sigma, Vt = svds(R_train_norm, k=50)
sigma = np.diag(sigma)

# Predict on test set
test_predictions = []
test_actuals = []

for _, row in test_data.iterrows():
    user_idx = row['userId'] - 1
    item_idx = R_train.columns.get_loc(row['movieId'])

    if user_idx < U.shape[0] and item_idx < Vt.shape[1]:
        pred = np.dot(np.dot(U[user_idx, :], sigma), Vt[:, item_idx]) + user_mean[user_idx]
        test_predictions.append(pred)
        test_actuals.append(row['rating'])

# Calculate RMSE
rmse = np.sqrt(mean_squared_error(test_actuals, test_predictions))
print(f"RMSE: {rmse:.4f}")
# Output: RMSE: 0.8734 (lower is better, typical range 0.8-1.0)

Alternating Least Squares (ALS)

SVD works well but has limitations with sparse data. ALS is an iterative optimization technique that's more robust and parallelizable.

How ALS Works

Initialize user and item matrices randomly

Fix item matrix, optimize user matrix

Fix user matrix, optimize item matrix

Repeat until convergence

Implementing ALS with Implicit

python

import implicit
from scipy.sparse import csr_matrix

# Convert to sparse matrix (user × item)
sparse_ratings = csr_matrix((ratings['rating'].values,
                             (ratings['userId'].values - 1,
                              ratings['movieId'].values - 1)))

# Create ALS model
model = implicit.als.AlternatingLeastSquares(
    factors=50,           # Number of latent factors
    regularization=0.1,   # L2 regularization
    iterations=20,        # Number of iterations
    calculate_training_loss=True
)

# Train the model
model.fit(sparse_ratings)

# Get recommendations for user
user_id = 0  # Zero-indexed
recommendations = model.recommend(user_id, sparse_ratings[user_id], N=10)

# recommendations is a list of (item_id, score) tuples
for item_id, score in recommendations:
    movie_title = movies[movies['movieId'] == item_id + 1]['title'].values[0]
    print(f"{movie_title}: {score:.4f}")

Factorization Machines: Adding Side Features

Matrix Factorization only uses user-item interactions. But what about:

User features: age, gender, location

Item features: genre, year, director

Context: time of day, device, season

Factorization Machines (FM) model interactions between all features!

FM Mathematical Foundation

Instead of just modeling user × item, FM uses this equation:

Prediction = Global Bias + Linear Terms + Pairwise Interactions

code

y_pred = w_0 + SUM(w_i * x_i) + SUM(SUM(<v_i, v_j> * x_i * x_j))
                i=1 to n         i=1  j=i+1

Breaking it down:

**w_0** = Global bias (baseline prediction)

**SUM(w_i * x_i)** = Linear terms (first-order interactions)

**SUM(SUM(<v_i, v_j> * x_i * x_j))** = Pairwise interactions (second-order)

Where:

**v_i, v_j** are k-dimensional latent vectors for features i and j

**<v_i, v_j>** is their dot product, modeling interaction strength

This allows modeling feature interactions even with sparse data

Key Advantage: FM can model interactions between features that never co-occurred in training data by learning latent vectors!

Implementing FM with xLearn

python

import xlearn as xl
import pandas as pd

# Prepare data in LIBSVM format
# Format: label feature1:value1 feature2:value2 ...

def prepare_fm_data(ratings, movies, users):
    """
    Convert rating data to FM format

    Features:
    - user_id (categorical)
    - movie_id (categorical)
    - genre_* (binary for each genre)
    - user_age_group (categorical)
    - rating_year (numerical)
    """
    fm_data = []

    for _, row in ratings.iterrows():
        user_id = row['userId']
        movie_id = row['movieId']
        rating = row['rating']

        # Get movie genres
        movie_row = movies[movies['movieId'] == movie_id].iloc[0]
        genres = movie_row['genres'].split('|')

        # Get user info (if available)
        user_row = users[users['userId'] == user_id].iloc[0]
        age_group = user_row['age_group']

        # Build feature string
        features = []
        features.append(f"0:{user_id}")  # user ID
        features.append(f"1:{movie_id}")  # movie ID
        features.append(f"2:{age_group}")  # user age group

        # Add genre features (offset by 1000 to avoid ID collision)
        for i, genre in enumerate(genres):
            features.append(f"{1000 + i}:1")

        # Create FM row: label feature1:value1 feature2:value2 ...
        fm_row = f"{rating} {' '.join(features)}"
        fm_data.append(fm_row)

    return fm_data

# Save to file
fm_data = prepare_fm_data(ratings, movies, users)
with open('fm_train.txt', 'w') as f:
    f.write('
'.join(fm_data))

# Train FM model
fm_model = xl.create_fm()
fm_model.setTrain("fm_train.txt")

# Hyperparameters
param = {
    'task': 'reg',          # Regression task
    'lr': 0.2,              # Learning rate
    'lambda': 0.002,        # Regularization
    'k': 50,                # Latent factor dimension
    'epoch': 20,            # Number of epochs
    'metric': 'rmse'
}

# Train
fm_model.fit(param, './model.out')

# Predict
fm_model.setTest("fm_test.txt")
fm_model.setSigmoid()
fm_model.predict("./model.out", "./output.txt")

When to Use Factorization Machines

Use FM when:

You have rich side features (user demographics, item metadata)

Context matters (time, location, device)

You want to model feature interactions

Cold-start is a concern (new users/items with features)

Stick with MF when:

You only have interaction data

Simplicity and speed are priorities

Dataset is very large (FM is slower)

Handling Implicit Feedback

Most real-world systems don't have explicit ratings—they have clicks, views, purchases.

Key Differences

Explicit Feedback (ratings):

Clear preference signal

Sparse (users rate few items)

Interpretation: rating = preference strength

Implicit Feedback (clicks, views):

Abundant data (every action is recorded)

No negative feedback (absence ≠ dislike)

Interpretation: confidence in preference

Implicit ALS Implementation

python

import implicit
from scipy.sparse import csr_matrix

# Convert clicks/views to confidence scores
# More interactions = higher confidence
user_item_interactions = clicks_df.groupby(['userId', 'itemId']).size().reset_index(name='count')

# Build sparse matrix
sparse_interactions = csr_matrix(
    (user_item_interactions['count'].values,
     (user_item_interactions['userId'].values,
      user_item_interactions['itemId'].values))
)

# Create implicit ALS model
model = implicit.als.AlternatingLeastSquares(
    factors=100,
    regularization=0.01,
    iterations=50,
    alpha=40  # Confidence scaling factor (tune this!)
)

# Train
model.fit(sparse_interactions)

# Get similar items
item_id = 42
similar_items = model.similar_items(item_id, N=10)

for similar_item, score in similar_items:
    print(f"Item {similar_item}: {score:.4f}")

Tuning the Alpha Parameter

python

# Alpha controls how confidence scales with interaction count
# confidence = 1 + alpha * count

# Low alpha (1-10): Treat 1 click and 10 clicks similarly
# Medium alpha (10-40): Moderate scaling (recommended starting point)
# High alpha (40-100): Heavy users dominate

# Tune via cross-validation
best_alpha = None
best_metric = float('inf')

for alpha in [1, 5, 10, 20, 40, 80]:
    model = implicit.als.AlternatingLeastSquares(factors=50, alpha=alpha)
    model.fit(sparse_train)

    # Evaluate on validation set
    metric = evaluate_implicit_model(model, sparse_val)

    if metric < best_metric:
        best_metric = metric
        best_alpha = alpha

print(f"Best alpha: {best_alpha}, Metric: {best_metric:.4f}")

Production Optimizations

1. Approximate Nearest Neighbors

Computing exact similarities is slow. Use ANN for fast lookups.

python

import annoy

# Build ANN index for item embeddings
item_factors = model.item_factors  # From ALS model
n_factors = item_factors.shape[1]

# Create Annoy index
ann_index = annoy.AnnoyIndex(n_factors, metric='angular')

# Add items
for item_id in range(item_factors.shape[0]):
    ann_index.add_item(item_id, item_factors[item_id])

# Build index (more trees = better accuracy, slower build)
ann_index.build(n_trees=50)

# Save for serving
ann_index.save('item_ann.index')

# Fast similar item lookup
similar_items = ann_index.get_nns_by_item(
    item_id=42,
    n=10,
    include_distances=True
)

print(similar_items)
# Output: ([42, 156, 293, 87, ...], [0.0, 0.12, 0.15, 0.18, ...])

2. Precompute Recommendations

python

# Precompute top-100 recommendations for all users
# Update nightly or weekly

import pickle

recommendations_cache = {}

for user_id in range(n_users):
    recs = model.recommend(user_id, sparse_user_items[user_id], N=100)
    recommendations_cache[user_id] = recs

# Save to fast storage (Redis, DynamoDB, etc.)
with open('recommendations_cache.pkl', 'wb') as f:
    pickle.dump(recommendations_cache, f)

# At serving time, load from cache
with open('recommendations_cache.pkl', 'rb') as f:
    cache = pickle.load(f)

user_recs = cache.get(user_id, default_recommendations)

3. Online Updates

python

# Incrementally update user embeddings without full retraining

def update_user_embedding(user_id, new_interactions, model):
    """
    Update user embedding based on new interactions
    Uses online gradient descent
    """
    user_vector = model.user_factors[user_id].copy()
    item_factors = model.item_factors

    learning_rate = 0.01
    regularization = 0.1

    for item_id, confidence in new_interactions:
        item_vector = item_factors[item_id]

        # Prediction error
        prediction = np.dot(user_vector, item_vector)
        error = confidence - prediction

        # Gradient update
        user_vector += learning_rate * (
            error * item_vector - regularization * user_vector
        )

    # Update model
    model.user_factors[user_id] = user_vector

    return user_vector

Evaluation Beyond RMSE

RMSE doesn't capture everything. Consider:

Diversity

python

def diversity_score(recommendations):
    """
    Measure diversity in genre coverage
    """
    genres = set()
    for item_id in recommendations:
        item_genres = movies[movies['movieId'] == item_id]['genres'].values[0].split('|')
        genres.update(item_genres)

    return len(genres)  # More genres = more diverse

Novelty

python

def novelty_score(recommendations, item_popularity):
    """
    Measure how obscure recommended items are
    """
    novelties = []
    for item_id in recommendations:
        # -log(popularity): Popular items have low novelty
        novelty = -np.log2(item_popularity[item_id] + 1e-10)
        novelties.append(novelty)

    return np.mean(novelties)

Serendipity

python

def serendipity_score(recommendations, user_history, expected_recs):
    """
    Measure unexpected but relevant recommendations
    """
    # Items that are recommended but not expected
    unexpected = set(recommendations) - set(expected_recs)

    # Items user hasn't seen before
    novel = set(recommendations) - set(user_history)

    # Serendipity = unexpected AND novel
    serendipitous = unexpected & novel

    return len(serendipitous) / len(recommendations)

Key Takeaways

Matrix Factorization (SVD/ALS):

Pros: Handles sparsity, scalable, captures latent patterns

Cons: Cold-start for new users/items, black-box representations

Use when: You have interaction data at scale

Factorization Machines:

Pros: Incorporates side features, handles cold-start

Cons: Slower training, more complex

Use when: You have rich features, context matters

Production Tips:

Start with item-based CF or ALS as baseline

Use ANN for fast similarity search

Precompute recommendations for frequent access

Monitor diversity and novelty, not just accuracy

Update models regularly (daily/weekly)

What's Next?

In Part 3, we'll cover cutting-edge techniques:

Deep Learning: Neural collaborative filtering, autoencoders

Session-Based: RNNs for sequential recommendations

Multi-Armed Bandits: Exploration vs exploitation

Production Architecture: Building recommendation services at scale

These modern approaches power today's most sophisticated recommendation systems at companies like YouTube, TikTok, and Alibaba.

Questions about Matrix Factorization or Factorization Machines? Let's connect on [LinkedIn](https://www.linkedin.com/in/prashantjha-ds)!